공부중
역학적 에너지 보존(단진자) 본문
물리계에서 에너지의 형태는 변화될 수 있지만 그 총량을 항상 일정하며, 이를 역학적 에너지 보존이라 한다.
에너지는 운동 에너지, 퍼텐셜에너지, 열에너지, 전기에너지, 화학에너지 등으로 존재할 수 있다.
이번 단진자를 사용한 역학적 에너지 보존 실험에서는 에너지가 운동 에너지와 위치 에너지로의 변환만 나타난다고 가정하고 실험을 진행할 것이다.
1. 실험 이론

질량 m이 임의의 위치에서 가지는 에너지는 위치에너지 U 와 운동에너지 K의 합으로 나타나게 된다.

또한 에너지 보존 법칙에 의해 임의의 지점에서 전체 에너지의 총량은 동일하다.

최저점에서의 위치에너지는 0이므로 이때의 속력 v0는 다음과 같다.

2. 실험
실험에서 사용한 실험 장치는 다음과 같다.
 |
 |
단진자의 위치 h1의 값을 변화시키며 실험을 진행할 것이다. 모든 계산은 진자의 중심을 기준으로 계산되지만 실험에서 중심을 측정하는 것은 어려우므로 진자의 밑 부분을 기준으로 잡아 측정한다. 진자의 밑 부분을 기준으로 잡으면 바닥면에서 추의 밑 부분까지의 길이를 측정하여 실험 조건을 구할 수 있다.
추가로 만약 면도날의 위치를 변화시키지 않는다면 바닥면에서 면도날 까지의 위치를 측정한 뒤 진자의 지름을 빼는 방법을 사용하여 H의 값을 구할 수 있을 것이다.
이때 실험에서 측정은m0 h1, H, X를 측정할 것이며 각각이 의미하는 바는 다음과 같다.
| m0 : 추의 질량 [kg] h1 : 진자의 최저점와 최고점 사이의 위치 변화량 [m] H : 진자의 최저점에서의 진자의 위치 [m] X : 진자의 최저점에서 실을 끊었을때 진자가 최저점에서의 운동에너지로 낙하한 위치. 진자의 운동 에너지를 계산하기 위한 거리 X. [m] |
1) . 위치에너지라는 것이 어떠한 절대값일 것인데 위치 에너지 계산을 h1+H로 하는 것이 아니라 h1으로만 하는 이유 ?
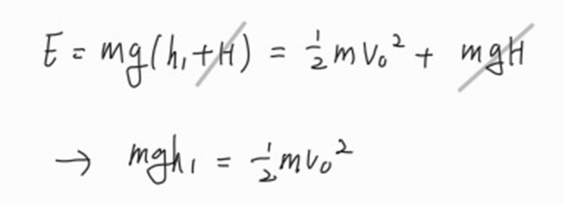
위의 식에 의해 역학적 에너지 보존이 계산되므로, H의 길이, 즉 면도날의 위치를 각 실험 횟수마다 변화시키는 것이 가능하다.
2) 최저점에서의 속도 구하는 법.
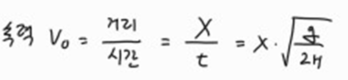
추가 낙하한 시간을 t라 할때,
 |
이므로
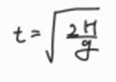
이다. t를 위의 식에 대입하여 최저점에서의 속력을 구할 수 있다.
참고 : 양조교
https://www.youtube.com/watch?v=XxVTJT2B1_E
https://www.youtube.com/watch?v=Hpn530NxfZQ&t=611s
'물리 > 일반물리학실험' 카테고리의 다른 글
| 선 운동량 보존 (탄성 충돌) (0) | 2024.05.12 |
|---|---|
| 탄도 진자( 탄동 진자) (0) | 2024.05.11 |
| 구심력 (0) | 2024.05.09 |
| 정지 마찰 계수 (0) | 2024.05.08 |
| 보다 진자(Borda)를 이용한 중력 가속도 측정 (0) | 2024.05.07 |

