공부중
[회로이론 1] 무전원 RLC 병렬회로 본문
9장
인덕터 커패시터 저항이 모두 있는 회로를 RLC 회로라 한다.
발진기 및 주파수 필터 등에 응용할 수 있다. 개인적인 생각으로 케이던스 시뮬레이션보다 psim 시뮬레이션 정확도가 더 높은 것 같다.
1. 무전원 RLC 병렬 회로
인덕터와 커패시터는 에너지를 저장하고 방출하며 시간의 변화에 따라 발진이 발생한다. 이상적으로 인덕터와 커패시터는 에너지를 소비하지 않으므로 발산하고, 저항은 에너지를 소산하여 damping을 유발한다.

1.1 미분방정식
위의 회로에서 마디( 노드 ) 방정식, KCL을 사용하면

이고, 이 경우에는 인덕터와 커패시터의 전압이 0이 아닌 초기값이 존재한다.

[식 1]의 양변을 시간에 대해 미분하면

이다. 이 식을 풀어 고유 응답을 구할 수 있다.
1.2 미분방정식 자연응답 구하기
미분방정식의 해가 다음과 같다고 가정한다.

따라서 [식 1]에 대입하면

이고, 이 방정식이 모든 시간에 대해 만족하려면 세가지 요소 중 적어도 1개는 0이 되어야 한다. 즉 A나 e^2t 또는 ( )이 되어야 한다. 하지만 A나 e^2t 이 0일 경우 미분방정식의 해를 가정한 이유가 없으므로 ( )의 값이 0이 되어야 한다.

이를 특성 방정식(또는 보조방정식)이라 부른다.
이는 이차 방정식의 형태이므로 우리가 아는 근의 공식으르 사용하여 위의 식이 0이 되게 하는 s 값을 구할 수 있으며
식 추가
근의 공식을 변형한 결과 ( 이 부분은 (https://brush-up.tistory.com/247) 이 글을 참고한다. )
 |
|
를 얻을 수 있다.
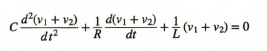
따라서 고유 응답은
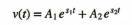
1.3
앞에서 (https://brush-up.tistory.com/247) 를 참고한다.
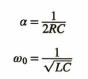
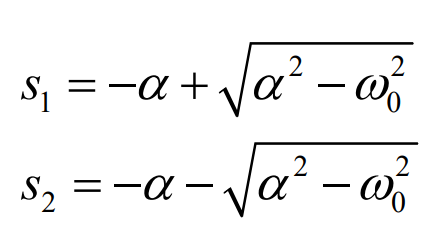
1.2의 s는 위와 같이 표현될 수 있으며 감쇠계수와 공진주파수의 값의 대소로 인해 다음과 같이 분류할 수 있다.
If α>ω0 the solutions are real, unequal and the response is termed overdamped
If α<ω0 the solutions are complex conjugates and the response is termed underdamped.
If α = ω0 the solutions are real and equal and the response is termed critically damped.
1.4 상수 A 값 구하기
'전자전기 > 회로 이론' 카테고리의 다른 글
| [회로이론 1] 무전원 RLC 직렬 회로 (0) | 2024.05.31 |
|---|---|
| [회로이론 1] 주파수 용어 정의 (0) | 2024.05.30 |
| [회로이론1] General RC / RL Circuits (2) (0) | 2024.05.20 |
| [회로이론1] Basic RC / RL Circuits (2) 충전 (0) | 2024.05.19 |
| [회로이론1] Basic RC / RL Circuits (1) 방전 (0) | 2024.05.19 |








