공부중
[회로이론1] 5장 회로 해석 (1) 선형성과 중첩의 원리 본문
회로이론 1에서 다루는 소자는 모두 선형소자이므로 회로는 선형회로이다.
따라서 중첩의 원리에 따라 2개이상의 독립 전원이 있는 회로에서의 응답을 각 독립전원이 하나만 있을 때의 응답들의 합으로 구할 수 있다.
간단히 중첩의 원리를 적용해보면 다음과 같다.
| 1. 어떤 i(t)가 v(t)를 생성하면, K* i(t)가 K*v(t)를 생성한다. 2. i1(t)가 v1(t)를 생성하고, i2(t)가 v2(t)를 생성하면, i1(t)+ i2(t) 가 v1(t)+ v2(t) 를 생성한다. |
종속 전원은 선형 요소가 도기 위한 선형 제어 방정식(linear control equation)이 필요하다.
1. 중첩의 원리( Superposition )예제
우리는 아래와 같은 회로에서 v1에 a 전원과 b전원이 얼마나 영향을 미치는지, 기여도에 대해 알아볼 것이다. 이를 위해 중첩의 원리를 이용할 것이다.
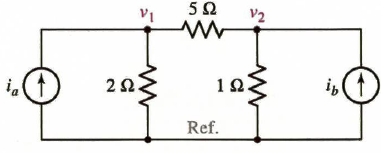
먼저 단순히 mesh 방정식이나 노드 방정식을 풀어서 v1과 v2의 값을 구할 수 있다.
 여기서 앞의 2x2 행렬을 A 라 할 때 |
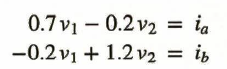 |
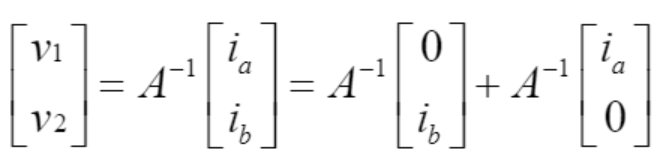 로 표현할 수 있으며, 오른쪽 식의 Expersiment B와 Expersiment A로 식을 나눌 수 있다. 즉, 앞에서 확인한 바와 같이 중첩의 원리를 사용하여 각 소스가 전압에 기여하는 정도를 계산할 수 있다는 의미이다. |
  |
 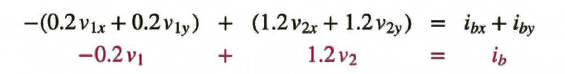 |
즉, 우리는 하나의 전원을 인가하고 다른 전원은 인가하지 않은 상태(off, 0)로 회로에 미치는 영향을 확인한 후 각 전원에 대한 결과를 모두 합하여 전체 전원이 해당 회로의 소자에 미치는 영향에 대해 분석할 수 있다.
사실 중첩의 원리에 의해 모두 0으로 만들지 않고 회로 해석을 해도 무방하지만 0으로 만들면 회로 해석이 간단하다는 이점이 있다.
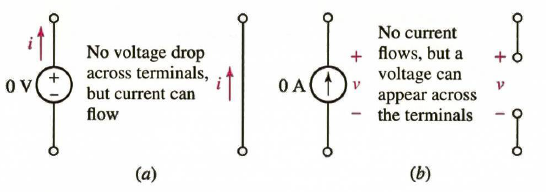
이때 전원을 off 할 경우, 전압원의 경우 단락(short)하고, 전류원은 open 시킨 등가회로를 구성하여 회로를 해석할 수 있다.
2. Superposition Example
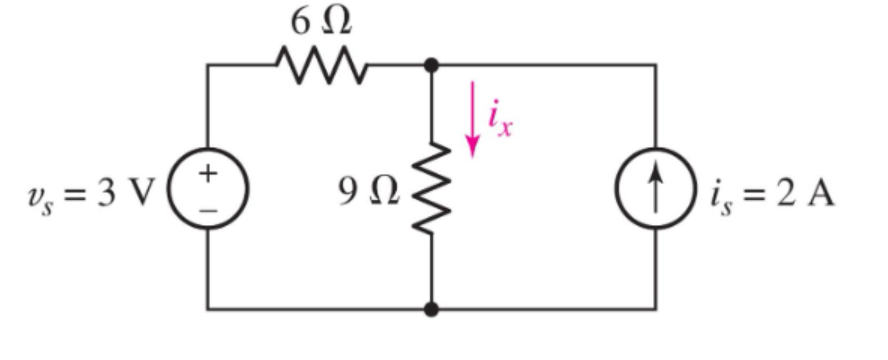
| 전압원이 미치는 영향 | 전류원이 미치는 영향 |
 |
 |
 |
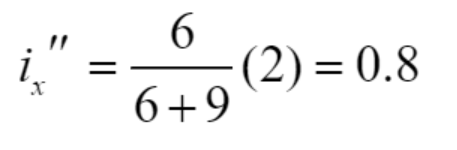 |
따라서 i_x의 값은 두 기여도를 모두 합하여 다음과 같이 구할 수 있다.
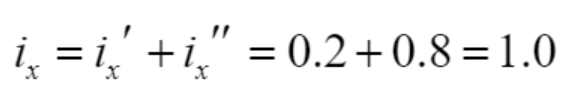
3. Superposition with a Dependent Source
그렇다면 종속 전원이 있을때 어떻게 중첩의 원리를 적용할 수 있을까?
앞에서 한 전원을 켜고, 다른 전원은 모두 off 시켜 회로를 해석했었다. 하지만 종속 전원의 경우 off 시켜서는 안되며, element로 인식하는것이 올바르다.
아래와 같은 회로를 해석해보자.
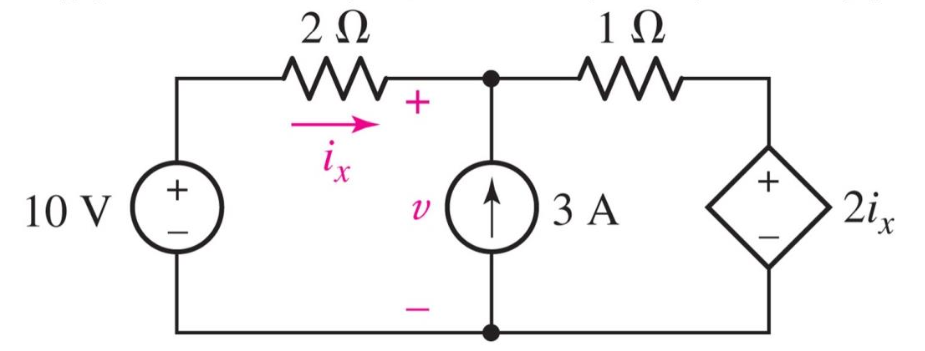
| 전압원이 미치는 영향 | 전류원이 미치는 영항 |
 |
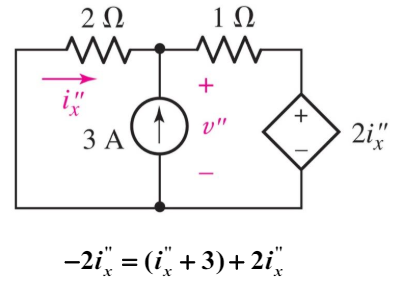 KVL을 사용해서 해석. |
두 결과를 합하여 i 값을 구할 수 있다.
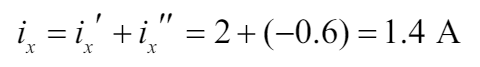
'전자전기 > 회로 이론' 카테고리의 다른 글
| [회로이론1] 5장 회로 해석 (3) Source Transformation (1) | 2024.04.28 |
|---|---|
| [회로이론1] 5장 회로 해석 (2) Power (1) | 2024.04.27 |
| [회로이론1] 회로 해석(3) Mesh analysis (0) | 2024.04.19 |
| [회로이론1] 회로 해석(2) Nodal analysis (0) | 2024.04.18 |
| [회로이론1] 회로 해석 방법 (1) (0) | 2024.04.17 |



