공부중
[회로이론1] Basic RC / RL Circuits (1) 방전 본문
hyat 회로이론 8장
1. 무전원(Source-Free) RC 회로의 전압 특성
커패시터는 전하는 저장하는 소자이다. 다음과 같은 전압 전류 관계식을 가진다.
 |
 |
따라서 회로 해석을 위해서는 미분 방정식을 풀이하고 해석할 수 있어야 한다.
아래 회로와 같이 초기 조건 (initial condition) (t=0에서 커패시터에 저장된 전압 = V0)인 RC 회로를 살펴보자
외부 전원이나 강제 함수가 없다고 가정하면 이 무전원 회로의 해는 자연 응답이 된다.
* 자연 응답 : 외부 전원이 없는 경우의 동작
 |
KCL을 사용하면   해 :  |
미분 방정식 해 구하기
1) 미분 방정식 구하기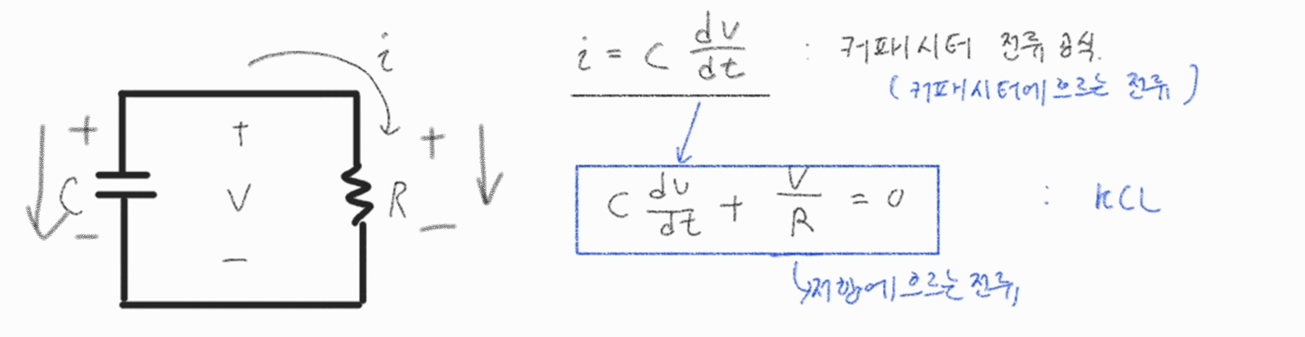 |
| 2) 미분 방정식 풀이 2.1 자연 응답 해( natural response ) ( 일반해 )  |
2.2 강제 응답 해( Forced Response ) , 특수 해 구하기  |
2.3 완전 응답  |
2.4 초기 조건 확인으로 A 값 구하기  |
결론적으로 무전원 RC 회로의 응답 특성은 다음과 같다
 |
 |
이때 RC를 시상수(The time constant , τ = RC) 라 한다.

2. The Exponential Response
무전원 RC 회로에서 C의 전압을 Exponential 한 특성을 가진다.
 |
 |

그러므로 τ = t 에서의 응답은 초기값이 36.8%로 떨어진다.
| - 전압이 0으로 감소하는 시간이 얼마나 걸리는가 ? -> 약 5τ. 이 시점에서 전압은 원래 값의 1% 미만으로 감소한다. |
3. 무전원(Source-Free) RL 회로의 전류 특성
인덕터의 전압 전류 관계식은 다음과 같다.

initial condition i(0) = I0
initial condition, i(0) = I0  |
미분 방정식 :   해 :  |
미분 방정식 해 구하기
1) 미분 방정식 구하기 |
| 2) 미분 방정식 풀이 2.1 자연 응답 해( natural response ) ( 일반해)  |
2.2 강제 응답 해( Forced Response ) , 특수 해 구하기  |
2.3 완전 응답  |
2.4 초기 조건 확인으로 A 값 구하기  |
결론적으로
 |
 |
이때 τ = L R 이다.

4. The Exponential Response

5. 이때 커패시터는 전압에 대한식을, 인덕터는 전류에 관한 식을 사용하는 이유가 무엇일까?

회로를 분석하고 미분방정식을 풀기 위해서는 초기조건이 필요하다. 즉, t = 0일떄의 값을 알고 있어야 한다.
커패시터의 전압값과 인덕터의 전류는 항상 연속적으로 변화하므로 미분값이 연속이다.
하지만 커패시터의 전류와 인덕터의 전압은 미분가능하지 않을 수 있다. 즉, 미분 한 함수가 불연속일 수 있다.

즉 위 표의 적분으로 표현된 값이 연속적으로 변화하게 될 것이며,
파랑으로 표시된 값으로 식을 전개해야 연속적인 초기값을 사용하게 되기 때문이다.

https://brush-up.tistory.com/193
[회로이론 1] Basic Component (1) ( 저항, 커패시터, 인덕터)
저항, 커패시터, 인덕터와 같은 소자들은 이후에 모두 임피턴스(Z, Impedance)로 등가화 할 수 있다. 각 소자의 특성에 대해 정리해보자. 1. 저항 먼저 기본적인 소자인 저항이다. 기본적인 공식인 옴
brush-up.tistory.com
'전자전기 > 회로 이론' 카테고리의 다른 글
| [회로이론1] General RC / RL Circuits (2) (0) | 2024.05.20 |
|---|---|
| [회로이론1] Basic RC / RL Circuits (2) 충전 (0) | 2024.05.19 |
| [회로이론 1] 회로 응답 (0) | 2024.05.18 |
| [회로 이론 1] 단위 계단 함수 (The Unit Step Function) (0) | 2024.05.11 |
| [회로이론1] 5장 회로 해석 (5) Δ-Y (delta-wye) Conversion (0) | 2024.04.30 |




