공부중
[DSM] 논문 : Sigma-Delta Modulators (2) Fundamentals of ΣΔ Modulators 본문
[DSM] 논문 : Sigma-Delta Modulators (2) Fundamentals of ΣΔ Modulators
복습 2024. 9. 11. 01:55Sigma-Delta Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey
(2) Fundamentals of ΣΔ Modulators :
D. Putting All Pieces Together: ΣΔ Modulation
E. Basic Architecture of a ΣΔ ADC
이전 글 : https://brush-up.tistory.com/304
Fundamentals of ΣΔ Modulators
D. Putting All Pieces Together: ΣΔ Modulation
D. Putting All Pieces Together: ΣΔ Modulation
Oversampling and noise-shaping can be used to build an ADC by embedding a quantizer in a feedback loop 6 as illustrated in Fig. 6—generally known as ΣΔM [2], [5], [6].7 Let us consider that the gain of the loop filter, H(z), is large inside the signal band and small outside it. Due to the action of the feedback, the input signal, x, and the analog version of the modulator output, y, will practically coincide within the signal band. Consequently, most of the differences between both signals will be placed at higher frequencies, i.e., the quantization error, eq, is shaped and most of its power is pushed outside the signal band. Assuming that the quantizer in Fig. 6 is represented by the linear, additive white noise model of Fig. 3(d), the feedback system in Fig. 6 can be viewed as a two-input, x and e, one-output, y, system, which can be represented in the Z-domain by8
{Y(z)} = {\hbox{STF}}(z) X(z) + {\hbox{NTF}}(z) E(z) \eqno{\hbox{(5)}}
오버샘플링과 노이즈 셰이핑은 그림 6에 나타난 대로 양자화기를 피드백 루프에 내장하여 ADC를 구축하는 데 사용할 수 있으며, 이는 일반적으로 ΣΔ 변조기(ΣΔM)라고 불립니다 [2], [5], [6]. 루프 필터 H(z)의 이득이 신호 대역 내에서 크고 그 외에서는 작다고 가정해봅시다. 피드백의 작용으로 인해 입력 신호 x와 변조기 출력의 아날로그 버전 y는 신호 대역 내에서 사실상 일치하게 됩니다. 따라서 두 신호 간의 대부분의 차이는 고주파수에 위치하게 되며, 즉 양자화 오류 eq가 형성되고 그 전력의 대부분이 신호 대역 밖으로 밀려납니다. 그림 6의 양자화기가 그림 3(d)의 선형 가산 백색 잡음 모델로 표현된다고 가정할 때, 그림 6의 피드백 시스템은 두 입력 x와 e, 하나의 출력 y를 가지는 시스템으로 볼 수 있으며, 이는 Z-도메인에서 다음과 같이 표현될 수 있습니다:

여기서 STF(z)\text{STF}(z)는 신호 전달 함수, NTF(z)\text{NTF}(z)는 잡음 전달 함수를 나타냅니다.
where X(z) and E(z) represent the Z-transform of x and e, respectively, and STF(z) and NTF(z) stand for the signal- and noise transfer functions, respectively given by
{\hbox{STF}}(z)= {g_qH(z) \over 1+g_qH(z)}; {\hbox{NTF}}(z)= {1 \over 1+g_qH(z)} \eqno{\hbox{(6)}}
Note that, if the loop filter is designed such that |H(f)|→∞ within the signal band, then |STF(f)|→1 and |NTF(f)|→0, i.e., the input signal is allowed to pass whereas the quantization error is ideally cancelled. However, the error cannot be completely nulled in practice because H(z) has a limited gain, and the in-band noise power is given by (4), whenever H(z) is defined so that NTF(z) is given by (3).
여기서 X(z) 와 E(z) 는 각각 xx와 ee의 Z-변환을 나타내며, STF(z)\text{STF}(z)와 NTF(z)\text{NTF}(z)는 각각 신호 전달 함수와 잡음 전달 함수를 의미합니다. 이들은 다음과 같이 주어집니다:


루프 필터가 신호 대역 내에서 ∣H(f)∣→∞|H(f)| \rightarrow \infty가 되도록 설계된 경우, ∣STF(f)∣→1|STF(f)| \rightarrow 1이 되고 ∣NTF(f)∣→0|NTF(f)| \rightarrow 0이 됩니다. 즉, 입력 신호는 통과하도록 허용되며 양자화 오류는 이상적으로 취소됩니다. 그러나 실제로는 H(z)의 이득이 제한적이기 때문에 오류를 완전히 제거하는 것은 불가능하며, H(z)가 (3)에 의해 주어진 NTF(z)로 정의될 때마다 밴드 내 잡음 전력은 (4)에 의해 주어집니다.
진폭 AxA_x의 사인파 입력 신호를 가정할 때, 변조기 출력에서의 신호 대 잡음비(SNR)와 동적 범위(DR)는 다음과 같이 주어집니다:
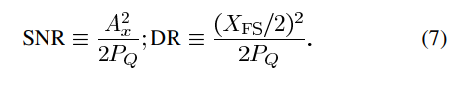
여기서 PQP_Q는 밴드 내 양자화 잡음 전력을 나타내며, XFSX_{\text{FS}}는 전체 스케일(full scale) 출력을 의미합니다.
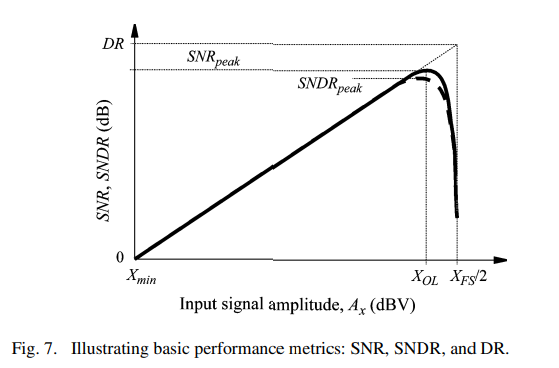
The above performance metrics are conceptually represented in Fig. 7. Note that SNR increases with Ax until Ax reaches the overload level, XOL. Beyond this level the quantizer input frequently goes outside the nonoverload range of the quantizer and hence the SNR curve drops sharply. As will be discussed in Section IV, the ideal performance depicted in Fig. 7 is degraded as a consequence of other error contributions—both linear and nonlinear—to the in-band error power, apart from quantization error. To take into account all these errors, the signal-to-(noise plus distortion) ratio (SNDR) is defined [26]. The maximum values of SNR and SNDR are often called SNRpeak and SNDRpeak, respectively illustrated in Fig. 7. Replacing the expression (4) in (7), the ideal value of DR expressed in dB gives
{{\hbox{DR}} \vert_{{\rm dB}}} = 10\log \left[{3(2^B-1)^2(2L+1){\hbox{OSR}}^{2L+1} \over 2\pi^{2L}} \right]. \eqno{\hbox{(8)}}
위의 성능 지표는 그림 7에서 개념적으로 표현되어 있습니다. SNR은 Ax가 과부하 수준인 XOL에 도달할 때까지 증가합니다. 이 수준을 넘어서면 양자화기 입력이 자주 양자화기의 비과부하 범위를 벗어나므로 SNR 곡선이 급격히 떨어집니다. 제 IV장에서 논의될 것처럼, 그림 7에 묘사된 이상적인 성능은 양자화 오류 외에도 밴드 내 오류 전력에 기여하는 다른 오류(선형 및 비선형)의 결과로 저하됩니다. 이러한 모든 오류를 고려하기 위해 신호 대 (잡음 플러스 왜곡) 비율(SNDR)이 정의됩니다 [26]. SNR과 SNDR의 최대 값은 각각 SNRpeak와 SNDRpeak로 불리며, 그림 7에서 설명됩니다. 식 (4)를 (7)에 대입하면, dB 단위로 표현된 DR의 이상적인 값은 다음과 같습니다:
DR_dB = 10log [(3(2^B-1)^2*(2L+1)OSR^(2L+1)) / (2pi^(2L))] (8)
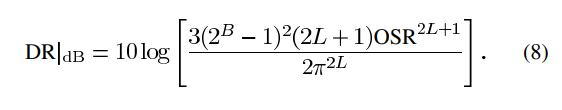
이상적인 N비트 나이퀴스트율 ADC의 동적 범위(DR) 식은 B=N, L=0 및 OSR=1을 위의 식에 대입함으로써 얻을 수 있으며, 다음과 같은 결과를 제공합니다 [26]:
DR_dB ≈ 6.02N + 1.76 (9)
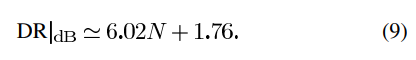
From (8) and (9), it can be established that the effective number of bits (ENOB)—defined as the number of bits needed for an ideal Nyquist-rate ADC to achieve the same DR as an ideal ΣΔ ADC—is given by [27] 11
\eqalignno{{{\hbox{ENOB}} \vert_{{\rm bits}}} & \equiv N\simeq {{\hbox{DR}}\vert_{\rm dB}-1.76 \over 6.02} \cr & \simeq \log _{2} \left[{(2^B-1)(2L+1) \over \pi ^{2L}}\right] \cr & \quad + \left(L+{1 \over 2}\right)\log_{2}({\hbox{OSR}}) & \hbox{(10)}}
(8)과 (9)에서, 효과적인 비트 수(ENOB)—이상적인 나이퀴스트율 ADC가 이상적인 ΣΔ ADC와 동일한 DR을 달성하기 위해 필요한 비트 수로 정의됨—는 다음과 같이 주어집니다 [27]:
ENOB_bits ≡ N ≈ (DR_dB - 1.76) / 6.02 ≈ log2 [(2^B-1)*(2L+1) / pi^(2L)] + (L + 1/2)*log2(OSR) (10)
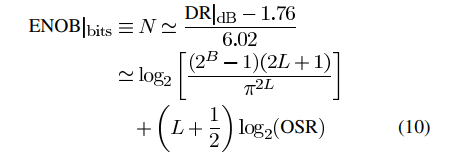
that means that a ΣΔM can achieve the same effective resolution as an ideal N-bit Nyquist-rate ADC by properly combining oversampling (OSR) and noise-shaping (L) to improve the accuracy of the embedded coarse quantization (typically B<5).
이는 ΣΔ 변조기가 적절한 오버샘플링(OSR)과 노이즈 셰이핑(L)의 조합을 통해 이상적인 N-비트 나이퀴스트율 ADC와 동일한 효과적인 해상도를 달성할 수 있음을 의미합니다. 이를 통해 일반적으로 5비트 미만인 조잡한 양자화의 정확성을 개선할 수 있습니다. 이 방법은 실제 양자화 과정에서 발생할 수 있는 잡음과 오류를 최소화하고, 전체 시스템의 해상도를 향상시키는 데 중요합니다. ΣΔ 변조기는 이러한 기술을 사용하여 낮은 비트 수에서도 고품질의 디지털 출력을 제공할 수 있습니다.
E. Basic Architecture of a ΣΔ ADC
E. Basic Architecture of a ΣΔ ADC
Fig. 8 shows the basic block diagram of a ΣΔ ADC, where Fig. 8(a) corresponds to a DT implementation (DT-ΣΔ ADC) and Fig. 8(b) is a continuous-time (CT) implementation (CT-ΣΔ ADC). In both cases, LP signals are assumed to be processed. Otherwise, the filters involved must be changed from LP to BP transfer functions.
E. ΣΔ ADC의 기본 구조
그림 8은 ΣΔ ADC의 기본 블록 다이어그램을 보여줍니다. 여기서 그림 8(a)는 디지털 타임(DT) 구현(DT-ΣΔ ADC)에 해당하고, 그림 8(b)는 연속 시간(CT) 구현(CT-ΣΔ ADC)을 나타냅니다. 두 경우 모두 저역통과(LP) 신호가 처리된다고 가정합니다. 그렇지 않으면 관련 필터는 저역통과에서 대역통과(BP) 전달 함수로 변경되어야 합니다.
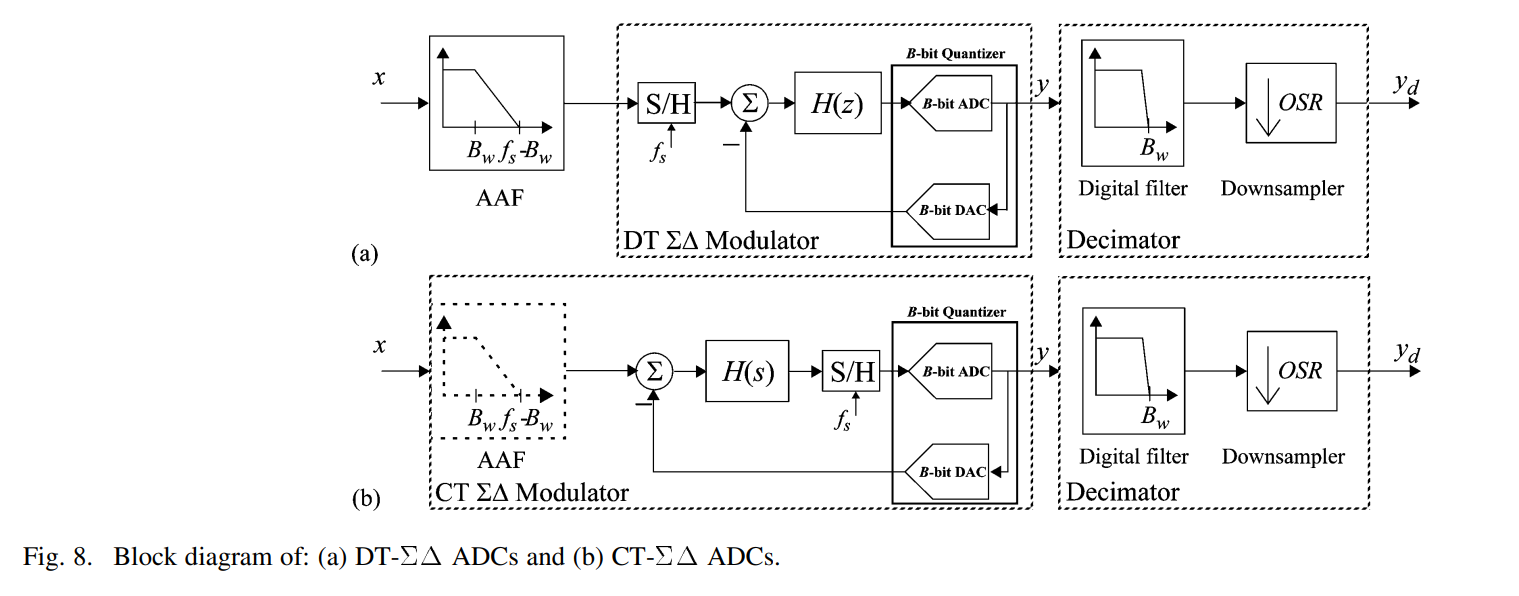
The scheme in Fig. 8 is made up of three main blocks: an AAF, a ΣΔM, and a decimator. Note from Fig. 8(b) that in the case of CT-ΣΔ ADCs, the input signal could be either subject to AAF or fed directly into the modulator without preceding any filtering. This can be done thanks to the implicit AAF which is embedded in CT-ΣΔMs [28]. Indeed, DT-ΣΔMs implement the sampling operation at the modulator input [Fig. 8(a)], whereas CT-ΣΔMs do it at the quantizer input and the loop filter is CT—see Fig. 8(b). Thus, the output signal is DT and a DT-to-CT transformation is needed to create the feedback signal. The process of reconstructing this signal, by using proper output pulse shape of the embedded digital-to-analog converter (DAC), plays a significant role on the overall CT-ΣΔM performance as will be discussed later [14].
그림 8의 구성은 세 가지 주요 블록으로 구성되어 있습니다: 안티에일리어싱 필터(AAF), ΣΔ 변조기(ΣΔM), 그리고 디시메이터입니다. 그림 8(b)에서 볼 수 있듯이, 연속 시간(CT) ΣΔ ADC의 경우, 입력 신호는 AAF를 거치거나 어떠한 필터링도 거치지 않고 직접 변조기로 공급될 수 있습니다. 이는 CT-ΣΔ 변조기에 내장된 암시적 AAF 덕분에 가능합니다 [28]. 실제로, 디지털 타임(DT) ΣΔ 변조기는 변조기 입력에서 샘플링 작업을 수행합니다 [그림 8(a)], 반면 CT-ΣΔ 변조기는 양자화기 입력에서 그 작업을 수행하며 루프 필터는 연속 시간입니다—그림 8(b) 참조. 따라서 출력 신호는 디지털 타임이며, 피드백 신호를 생성하기 위해 디지털 타임에서 연속 타임으로의 변환 작업이 필요합니다. 내장된 디지털-아날로그 변환기(DAC)의 적절한 출력 펄스 형태를 사용하여 이 신호를 재구성하는 과정은 나중에 논의될 것처럼 전체 CT-ΣΔ 변조기의 성능에 중요한 역할을 합니다 [14].
The output of the ΣΔM is a B-bit digital stream clocked at fs. The decimator, which is a purely digital block, removes the high-frequency components of the ΣΔM digital stream through high-selectivity digital filtering, and decimates to reduce the rate of the ΣΔM output stream down to the Nyquist frequency. Hence, the output of the ΣΔ ADC is a digitized version of the input signal—clocked at fN—with an equivalent resolution given by (10).
ΣΔ 변조기의 출력은 fs에서 동기화된 B비트 디지털 스트림입니다. 디시메이터는 순수하게 디지털 블록으로, ΣΔ 변조기 디지털 스트림의 고주파 성분을 고선택성 디지털 필터링을 통해 제거하고, ΣΔ 변조기 출력 스트림의 속도를 나이퀴스트 주파수까지 감소시키기 위해 데이터를 줄입니다. 따라서 ΣΔ ADC의 출력은 나이퀴스트 주파수 fN에서 동기화된 입력 신호의 디지털 버전으로, 식 (10)에 의해 주어진 동등한 해상도를 가집니다.
Out of the three blocks in Fig. 8, the ΣΔM is the most critical one, responsible for the accuracy of the whole ADC. For that reason, this paper will focus on this block, although taking into account that a ΣΔ ADC needs also the other two blocks [15].
그림 8의 세 블록 중에서 ΣΔ 변조기(ΣΔM)는 전체 ADC의 정확성을 담당하는 가장 중요한 블록입니다. 이러한 이유로, 이 논문은 이 블록에 중점을 두지만, ΣΔ ADC가 다른 두 블록도 필요로 한다는 점을 고려할 것입니다 [15].
https://ieeexplore.ieee.org/document/5672380
Sigma-Delta Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey
This paper presents a tutorial overview of <formula formulatype="inline" xmlns:mml="http://www.w3.org/1998/Math/MathML" xmlns:xlink="http://www.w3.org/1999/xlink"> <tex Notation="TeX">$\Sigma\Delta$</tex></formula> modulators, their operating principles an
ieeexplore.ieee.org
'시스템 반도체 설계 > Sigma-Delta Modulators' 카테고리의 다른 글
| [DSM] 논문 : Sigma-Delta Modulators (4) Nonideal Performance and Systematic Design (1) | 2024.09.13 |
|---|---|
| [DSM] 논문 : Sigma-Delta Modulators (3) Taxonomy of ΣΔ Modulators (1) | 2024.09.12 |
| [DSM] 논문 : Sigma-Delta Modulators (1) Introduction (1) | 2024.09.10 |
| [ΣΔMs] Sigma-Delta Modulators 의 기본 구조 (0) | 2024.02.28 |
| [ΣΔMs] Sigma-Delta Modulators (0) | 2024.02.27 |



