공부중
[DSM] 논문 : Sigma-Delta Modulators (3) Taxonomy of ΣΔ Modulators 본문
[DSM] 논문 : Sigma-Delta Modulators (3) Taxonomy of ΣΔ Modulators
복습 2024. 9. 12. 01:56Sigma-Delta Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey
(3) Taxonomy of ΣΔ Modulators
이전 글 : https://brush-up.tistory.com/305
Taxonomy of ΣΔ Modulators
ΣΔ 변조기의 분류
A large number of ΣΔM architectures have been reported in the open literature that implement some (or all) the following, nonexclusive, strategies to improve DR [6], [7]:
- IncreasingL. According to (8), for a given value of OSR, the increase in DR with L leads to ΔDR|dB≃10log{[(2L+3)/(2L+1)][OSR/π]2}. However, the use of high-order modulator loop filtering (usually L>3) gives rise to stability problems, and the necessary loop gain scaling worsens the performance below the ideal one.
- Increasing OSR leads to an increment of (L+1/2) bit/octave in the effective resolution. However, for wideband signals the use of high values of OSR is impractical, because of the prohibitive sampling frequencies required, with the subsequent penalty in power consumption.
- IncreasingB leads to an increase of 6 dB (1 bit) in DR for each extra bit in the quantizer [11]. However, the required multibit feedback DAC is not inherently linear.
ΣΔM(시그마-델타 변조기) 구조에 대한 많은 연구가 공개 문헌에서 보고되었으며, 동적 범위(DR)를 향상시키기 위한 다음과 같은 비독점적인 전략들을 일부(또는 전부) 구현하고 있습니다 [6], [7]:
L 증가. 식 (8)에 따르면, 주어진 OSR 값에 대해 L이 증가함에 따라 DR은 ΔDR|dB ≈ 10log{[(2L+3)/(2L+1)][OSR/π]2} 만큼 증가합니다. 그러나 고차 모듈레이터 루프 필터링(보통 L>3)의 사용은 안정성 문제를 야기하며, 필요한 루프 이득 조정은 이상적인 성능 이하로 성능을 악화시킵니다.
OSR 증가는 효과적인 해상도를 (L+1/2) 비트/옥타브 증가시킵니다. 그러나 광대역 신호의 경우 높은 OSR 값의 사용은 금지적인 샘플링 주파수 요구로 인해 비현실적이며, 그에 따른 전력 소비의 증가가 발생합니다.
B 증가는 양자화기의 추가 비트당 DR을 6 dB(1 비트) 증가시킵니다 [11]. 그러나 필요한 다중비트 피드백 DAC는 본질적으로 선형이 아닙니다.
The above strategies can be classified according to:
- The nature of the signals being handled, resulting in LP and BP ΣΔMs.
- The number of bits of the internal quantizers, dividing ΣΔMs into single-bit and multibit topologies.
- The number of quantizers employed. ΣΔMs employing only one quantizer are called single-loop structures, whereas those using several quantizers give rise to different topologies, namely: cascade, dual-quantization, etc.
- The circuit nature of the loop filter, classifying ΣΔMs into two main groups DT [Fig. 8(a)] and CT [Fig. 8(b)] implementations. According to this criterion, another type of ΣΔMs, called hybrid CT/DT ΣΔMs, tries to take advantage of the benefits of both circuit techniques [29]–[34].
위의 전략들은 다음과 같이 분류될 수 있습니다:
- 처리되는 신호의 성질에 따라, 저역통과(LP) 및 대역통과(BP) ΣΔ 변조기로 구분됩니다.
- 내부 양자화기의 비트 수에 따라, ΣΔ 변조기를 단일 비트 및 다중 비트 토폴로지로 나눕니다.
- 사용된 양자화기의 수에 따라, 단일 양자화기를 사용하는 ΣΔ 변조기는 단일 루프 구조라고 하며, 여러 양자화기를 사용하는 경우에는 캐스케이드, 이중 양자화 등 다양한 토폴로지가 생깁니다.
- 루프 필터의 회로 성질에 따라, ΣΔ 변조기를 주로 두 가지 그룹, 디지털 타임(DT) [그림 8(a)] 및 연속 타임(CT) [그림 8(b)] 구현으로 분류합니다. 이 기준에 따라, 두 회로 기술의 이점을 활용하려는 하이브리드 CT/DT ΣΔ 변조기라는 또 다른 유형의 ΣΔ 변조기도 있습니다 [29]–[34].
이전 분류에서 파생된 모든 가능한 ΣΔ 변조기 구조를 설명하는 것은 이 논문의 범위를 넘어섭니다. 이에 대한 자세한 연구는 많은 논문과 책에서 찾아볼 수 있습니다 [5]–[16]. 대신, 이 절은 가장 대표적인 ΣΔ 변조기 토폴로지의 가족들에 초점을 맞출 것입니다.
A. Low-Order Single-Loop ΣΔMs
A. Low-Order Single-Loop ΣΔMs
The simplest way of building a ΣΔM architecture is combining a DT forward-Euler (FE) integrator, i.e., H(z)=z−1/(1−z−1) as the loop filter with a single-bit quantizer, i.e., a comparator. The resulting architecture—known as first-order single-bit ΣΔM—is illustrated in Fig. 9(a). Assuming a linear model for the quantizer, the Z-transform of the modulator output is given by (5) with STF(z)=z−1 and NTF(z)=(1−z−1). This topology has two main disadvantages. On the one hand, DR increases with OSR at a rate of only 1.5-bit/octave, which implies using very high values of OSR to achieve medium-high effective resolutions. Another important drawback associated to first-order single-bit ΣΔMs is the presence of pattern noise and the so-called idle tones as illustrated in Fig. 10(a). This tonal behavior, which is present even considering ideal circuit components, is a direct consequence of the strong correlation existing between the input signal and the quantization error. This correlation leads to a colored quantization error, instead of a white noise and—in addition to causing a number of tones within the signal band—gives rise to an in-band error power higher than that predicted by the linear model [19], [22], [35].
A. 저차 단일 루프 ΣΔ 변조기
ΣΔ 변조기 구조를 구축하는 가장 간단한 방법은 DT 포워드-오일러(FE) 적분기, 즉 H(z)=z−1/(1−z−1)를 루프 필터로 사용하고 단일 비트 양자화기, 즉 비교기를 조합하는 것입니다. 이로 인해 생성되는 구조—첫 번째 차수 단일 비트 ΣΔ 변조기로 알려져 있습니다—는 그림 9(a)에서 보여집니다. 양자화기에 대해 선형 모델을 가정하면, 변조기 출력의 Z-변환은 STF(z)=z−1 및 NTF(z)=(1−z−1)로 주어집니다. 이 토폴로지는 두 가지 주요 단점을 가지고 있습니다. 한편으로는 DR이 OSR에 따라 1.5비트/옥타브의 비율로만 증가하기 때문에, 중간-높은 효과적 해상도를 달성하기 위해 매우 높은 OSR 값을 사용해야 합니다. 첫 번째 차수 단일 비트 ΣΔ 변조기와 관련된 또 다른 중요한 단점은 그림 10(a)에서 보여지는 것처럼 패턴 노이즈와 이른바 공회전 톤의 존재입니다. 이 톤 현상은 이상적인 회로 구성 요소를 고려하더라도 존재하며, 입력 신호와 양자화 오류 사이에 강한 상관관계가 있는 직접적인 결과입니다. 이 상관관계는 백색 잡음 대신 색이 있는 양자화 오류를 초래하며—신호 대역 내의 많은 톤을 유발할 뿐만 아니라—선형 모델이 예측한 것보다 높은 밴드 내 오류 전력을 야기합니다 [19], [22], [35].


The problems of Fig. 9(a) can be mostly avoided if the 1-bit quantizer in a first-order ΣΔM is replaced itself by a first-order ΣΔM as illustrated in Fig. 9(b). The resulting modulator is called second-order ΣΔM, which is stable if gDAC2=2gx1gDAC1 [36]. In that case, assuming gx1=gx2=1 and a white noise model for the quantizer, we obtain STF(z)=z−2 and NTF(z)=(1−z−1)2. Moreover, DR increases with OSR by 2.5-bit/octave, which significantly improves the performance of the first-order modulator in terms of the sampling frequency required. In addition, the use of two integrators also contributes to decorrelate the input signal and the quantization error, thus decreasing the presence of idle tones in the output spectrum as illustrated in Fig. 10(b).
그림 9(a)의 문제는 첫 번째 차수 ΣΔ 변조기의 1비트 양자화기를 그림 9(b)에서 보여지는 것처럼 첫 번째 차수 ΣΔ 변조기 자체로 대체하면 대부분 피할 수 있습니다. 결과적으로 생성된 변조기는 두 번째 차수 ΣΔ 변조기로 불리며, gDAC2=2gx1gDAC1일 경우 안정적입니다 [36]. 이 경우, gx1=gx2=1이라고 가정하고 양자화기에 대해 백색 잡음 모델을 사용하면, STF(z)=z−2 및 NTF(z)=(1−z−1)^2을 얻을 수 있습니다. 또한, DR은 OSR에 따라 2.5비트/옥타브로 증가하여 필요한 샘플링 주파수 측면에서 첫 번째 차수 변조기의 성능을 크게 향상시킵니다. 또한 두 개의 적분기의 사용은 입력 신호와 양자화 오류의 상관관계를 줄이는 데 기여하여 그림 10(b)에서 보여지듯이 출력 스펙트럼에서 공회전 톤의 존재를 감소시킵니다.
B. High-Order ΣΔMs
B. High-Order ΣΔMs
The concept underlying first- and second-order single-loop ΣΔMs can be extended towards Lth-order filtering, thus resulting in the modulator topology shown in Fig. 9(c), which is known as L-th order single-loop ΣΔM with distributed feedback. Using a linear model for the quantizer, it can be shown that STF(z)=z−L,NTF(z)=(1−z−1)L and DR is given by (8). However, this performance is not achieved in practice due to stability problems associated to pure differentiator NTFs, in which stability can only be conditionally guaranteed for a limited range of input amplitudes when L>2 [37]. In order to address this problem, alternative realizations of high-order single-loop ΣΔMs have been proposed that implement an IIR NTF [6], [7]. A pioneer topology using multiple feedforward and feedback analog paths was proposed by Lee and Sodini, synthesizing NTFs of the form NTF(z)=(z−1)L/D(z), with D(z) being a polynomial determined by the feedforward analog coefficients [38]. There are several implementations of this idea. As an illustration, Fig. 11 shows an example that consists of a 5th-order single-loop with an IIR NTF. This modulator—often referred to as cascade of resonators with distributed feedforward (CRFF)—sets STF(z)=1−NTF(z) [6]. Local resonation feedback coefficients (γ1,2) can be used to set additional notches in NTF(z) in order to increase the noise filtering without increasing the loop filter order.
B. 고차 ΣΔ 변조기
첫 번째 및 두 번째 차수 단일 루프 ΣΔ 변조기의 기본 개념은 L차 필터링으로 확장될 수 있으며, 그 결과 그림 9(c)에서 보여지는 변조기 토폴로지가 생성됩니다. 이는 분산 피드백이 있는 L차 단일 루프 ΣΔ 변조기로 알려져 있습니다. 양자화기에 대한 선형 모델을 사용하면, STF(z)=z^(-L), NTF(z)=(1−z^(-1))^L이며 DR은 식 (8)에 의해 주어집니다. 그러나 L>2일 때 입력 진폭의 제한된 범위에 대해서만 조건부로 안정성이 보장될 수 있는 순수 차별기 NTF와 관련된 안정성 문제로 인해 이 성능은 실제로 달성되지 않습니다 [37]. 이 문제를 해결하기 위해, IIR NTF를 구현하는 고차 단일 루프 ΣΔ 변조기의 대안적인 실현이 제안되었습니다 [6], [7]. 리와 소디니에 의해 제안된 선구적인 토폴로지는 다중 피드포워드 및 피드백 아날로그 경로를 사용하여 NTF(z)=(z^(-1))^L/D(z) 형태의 NTF를 합성하였으며, 여기서 D(z)는 피드포워드 아날로그 계수에 의해 결정되는 다항식입니다 [38]. 이 아이디어의 여러 구현이 있습니다. 예를 들어, 그림 11은 IIR NTF를 갖는 5차 단일 루프의 예를 보여줍니다. 이 변조기는 종종 분산 피드포워드가 있는 공진기 캐스케이드(CRFF)로 언급되며, STF(z)=1−NTF(z)로 설정됩니다 [6]. 지역 공진 피드백 계수 (γ1,2)를 사용하여 루프 필터 차수를 증가시키지 않고도 NTF(z)에 추가적인 노치를 설정하여 잡음 필터링을 증가시킬 수 있습니다.

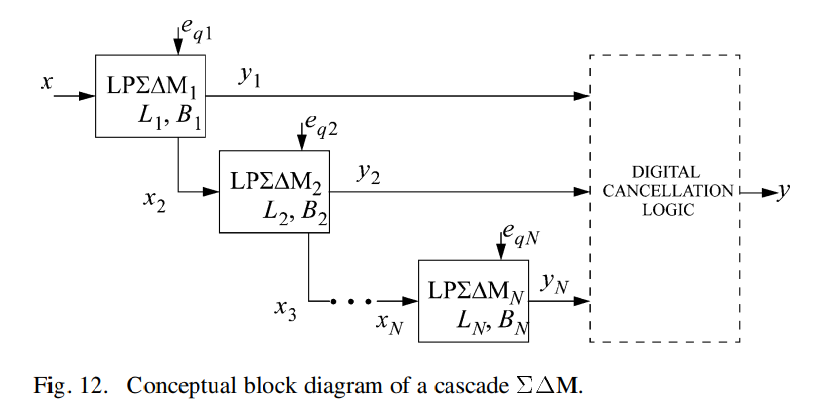
A common disadvantage of most high-order single-loop ΣΔM topologies implementing IIR NTFs is the increased circuit complexity due to the large number of analog coefficients required. A well-known alternative to circumvent instability while obtaining high-order noise-shaping consists of using the so-called MASH (multistage noise-shaping) ΣΔMs, often referred to as cascade or multistage ΣΔMs [6], [39]. This architecture is conceptually depicted in Fig. 12. Each stage, consisting of a low-order (typically either second or first order) single-loop ΣΔM, modulates a signal that contains the quantization error generated in the previous stage. Once in the digital domain, the stage outputs are processed and combined by a digital cancellation logic (DCL) so that only the quantization error of the last stage remains. Also, this error is shaped by a transfer function whose order equals the sum of the respective orders of all the stages in the cascade, i.e., L=L1+L2+⋯+LN. However, in practice, it is well known that the maximum number of stages—and consequently L—is limited by circuit nonidealities, particularly mismatch. This error causes incomplete cancellation of low-order quantization errors at the modulator output [15]. This effect—known as noise leakage—is especially critical in cascade CT-ΣΔMs because of their higher sensitivity to circuit element tolerances—a fact which may account for the small number of cascade CT-ΣΔM integrated circuits (ICs) reported so far [40]–[43].
대부분의 고차 단일 루프 ΣΔ 변조기 토폴로지에서 IIR NTF를 구현하는 경우 흔히 발생하는 단점은 필요한 아날로그 계수의 수가 많아서 회로 복잡성이 증가한다는 것입니다. 불안정성을 피하면서 고차 노이즈 셰이핑을 얻는 잘 알려진 대안은 이른바 MASH(다단계 노이즈 셰이핑) ΣΔ 변조기를 사용하는 것으로, 종종 캐스케이드 또는 다단계 ΣΔ 변조기로 언급됩니다 [6], [39]. 이 아키텍처는 개념적으로 그림 12에서 묘사됩니다. 각 단계는 낮은 차수(일반적으로 두 번째 또는 첫 번째 차수)의 단일 루프 ΣΔ 변조기로 구성되며, 이전 단계에서 생성된 양자화 오류가 포함된 신호를 변조합니다. 디지털 영역에서 한번, 각 단계의 출력은 디지털 취소 논리(DCL)에 의해 처리되고 결합되어 마지막 단계의 양자화 오류만 남습니다. 또한, 이 오류는 캐스케이드의 모든 단계의 차수 합과 같은 차수의 전달 함수에 의해 형성됩니다. 즉, L=L1+L2+⋯+LN입니다. 그러나 실제로는 회로의 비이상적인 특성, 특히 불일치로 인해 최대 단계 수와 결과적으로 L이 제한된다는 것이 잘 알려져 있습니다. 이 오류는 변조기 출력에서 저차 양자화 오류의 불완전한 취소를 야기합니다 [15]. 이 효과는 특히 캐스케이드 CT-ΣΔ 변조기에서 심각한데, 이는 회로 요소의 허용 오차에 더 높은 민감도를 가지기 때문입니다. 이는 지금까지 보고된 캐스케이드 CT-ΣΔM 집적 회로(IC)의 수가 적은 이유를 설명할 수 있습니다 [40]–[43].
C. Multibit and Dual-Quantization ΣΔMs
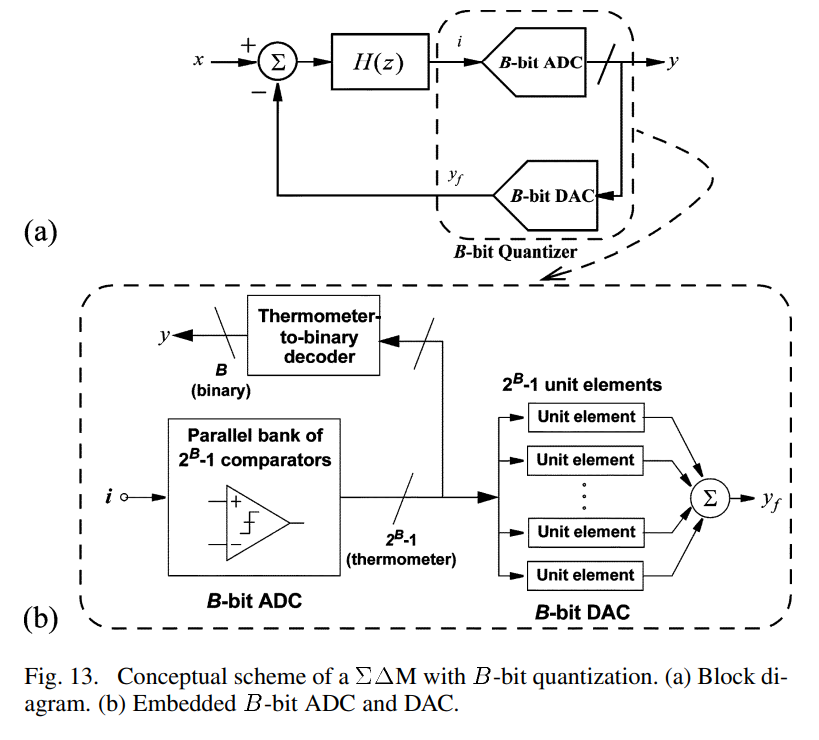
According to (10), an alternative way to improve the effective resolution consists of using embedded multibit (B>1) quantization—conceptually depicted in Fig. 13(a). As illustrated in Fig. 13(b), a multibit DAC commonly uses 2B−1 unit circuit elements (capacitors, resistors, current sources, etc.) to reconstruct the analog feedback signal in the modulator loop with 2B levels. Thus, the analog output level is generated by summing up the unit element outputs (usually charges or currents). Due to mismatches among different unit elements, a nonlinear input-output DAC characteristic is obtained. The nonlinear errors associated to the multibit feedback DAC are directly injected at the modulator input, thus degrading the modulator performance. Consequently, at least in single-loop topologies like the one conceptually depicted in Fig. 13(a), the embedded feedback DAC must be designed to reach the linearity targeted for the whole ΣΔ ADC [44].
C. 다중비트 및 이중 양자화 ΣΔ 변조기
(10)에 따르면, 효과적인 해상도를 향상시키는 대안적인 방법은 다중비트(B>1) 양자화를 사용하는 것입니다—개념적으로 그림 13(a)에 묘사되어 있습니다. 그림 13(b)에서 보여지듯, 다중비트 DAC은 일반적으로 2B−1개의 단위 회로 요소(커패시터, 저항, 전류원 등)를 사용하여 변조기 루프에서 아날로그 피드백 신호를 2B 레벨로 재구성합니다. 따라서 아날로그 출력 레벨은 단위 요소 출력(보통 전하 또는 전류)을 합산하여 생성됩니다. 서로 다른 단위 요소 간의 불일치로 인해 비선형 입력-출력 DAC 특성이 나타납니다. 다중비트 피드백 DAC과 관련된 비선형 오류는 변조기 입력에 직접 주입되어 변조기 성능을 저하시킵니다. 따라서, 그림 13(a)에서 개념적으로 묘사된 것과 같은 단일 루프 토폴로지에서는, 내장된 피드백 DAC은 전체 ΣΔ ADC의 목표로 하는 선형성에 도달하도록 설계되어야 합니다 [44].
A large number of strategies have been reported in order to achieve highly-linear multibit ΣΔMs, some of them requiring modest component matching [45]. Among other techniques, one of the most popularly used is the so-called dynamic element matching (DEM) [11], [44]. The basic idea behind DEM techniques consists of breaking the direct correspondence existing between the thermometer input code and their associated DAC output levels, so that the unit elements selected to generate a given DAC output level vary over time. This way, the fixed error of that level will be transformed into a time-varying error. To that purpose, a block is added to control the selection of elements at each clock cycle. The selection is done according to simple algorithms 12 that try to drive the average error in each DAC level to zero over time. Thus, part of the DAC error power that laid in the low-frequency range will be moved to higher frequencies, where it can be removed by the decimation filter.
다양한 전략들이 고도로 선형적인 다중비트 ΣΔ 변조기를 달성하기 위해 보고되었으며, 그 중 일부는 적절한 부품 매칭만을 요구합니다 [45]. 기타 기술 중에서도 가장 널리 사용되는 기술 중 하나는 소위 동적 요소 매칭(DEM)이라고 불립니다 [11], [44]. DEM 기술 뒤에 있는 기본 아이디어는 써모미터 입력 코드와 연관된 DAC 출력 레벨 사이에 존재하는 직접적인 대응 관계를 깨뜨려, 주어진 DAC 출력 레벨을 생성하는 단위 요소가 시간이 지남에 따라 변화하도록 하는 것입니다. 이 방식으로, 해당 레벨의 고정된 오류는 시간에 따라 변하는 오류로 변환됩니다. 이 목적을 위해, 각 클록 사이클에서 요소 선택을 제어하는 블록이 추가됩니다. 선택은 각 DAC 레벨에서 평균 오류를 시간에 따라 제로로 만들려고 시도하는 간단한 알고리즘 12에 따라 수행됩니다. 이렇게 하면, 저주파 범위에 있던 DAC 오류 전력의 일부가 높은 주파수로 이동되어, 여기서 디시메이션 필터에 의해 제거될 수 있습니다.
Other alternatives to reduce the impact of DAC nonlinearities are based on deterministic techniques, such as analog calibration [53], digital correction [54], and dual quantization. The latter consists of combining single-bit and multibit quantization in the same modulator topology in order to take advantage of the intrinsic linearity of 1-bit quantization and the reduced quantization error of multibit quantizers [15].
DAC 비선형성의 영향을 줄이기 위한 다른 대안들은 아날로그 보정 [53], 디지털 보정 [54], 그리고 이중 양자화와 같은 결정론적 기술에 기반을 두고 있습니다. 후자는 동일한 변조기 토폴로지에서 단일 비트와 다중 비트 양자화를 결합하여 1비트 양자화의 본질적인 선형성과 다중 비트 양자화기의 감소된 양자화 오류의 이점을 활용하는 것으로 구성됩니다 [15].
Since the original dual-quantizer general scheme was proposed by Leslie and Singh [55], illustrated in Fig. 14, there has been several ΣΔM topologies based on the same idea [56]. Among others, the most common approach consists of combining dual quantization and cascade topologies, so that only the last-stage quantizer is multibit, while the remaining ones are usually single-bit, i.e., B1=B2=⋯=BN−1=1 and BN>1 in Fig. 12. Therefore, the multibit DAC nonlinear errors are injected in the last stage of the cascade, so that the linearity requirements are relaxed because of the attenuation provided by the gain of the preceding stages within the signal band [57], [58].
레슬리와 싱에 의해 처음 제안된 이중 양자화 일반 스키마 [55], 그림 14에서 보여지듯이, 같은 아이디어에 기반한 여러 ΣΔM 토폴로지가 개발되었습니다 [56]. 그 중에서도 가장 일반적인 접근법은 이중 양자화와 캐스케이드 토폴로지를 결합하는 것으로, 마지막 단계의 양자화기만이 다중 비트이며 나머지는 보통 단일 비트입니다. 예를 들어, 그림 12에서 B1=B2=⋯=BN−1=1 이고 BN>1 입니다. 따라서, 다중 비트 DAC의 비선형 오류는 캐스케이드의 마지막 단계에 주입되므로, 신호 대역 내에서 앞 단계의 이득에 의해 제공되는 감쇠로 인해 선형성 요구 사항이 완화됩니다 [57], [58].

D. Bandpass ΣΔMs
BP-ΣΔMs are a particular class of ΣΔMs that place the zeroes of NTF(f) in a given bandwidth around an intermediate frequency (IF) location, usually named center or notch frequency, fn. Therefore, BP-ΣΔMs differ from their LP counterparts in that the loop filter is of BP type instead of LP type as illustrated in Fig. 15 [59]–[62]. This has an obvious application in the front-end of wireless communication systems. Indeed, BP-ΣΔMs are very suited for the implementation of ADCs in such systems because, compared with Nyquist-rate ADCs, BP-ΣΔMs do not need to digitize the whole Nyquist band (from dc to fs) (see Fig. 15). Instead, they digitize just the signal band, thereby requiring much lower power consumption to obtain a given DR [25], [63]. In addition, IF A/D conversion allows a great part of the signal processing to be moved from the analog domain to the digital domain, including: quadrature mixing, channel selection, gain control, and demodulation. This results in robust radiofrequency (RF) receivers with high degree of programmability and adaptability to a number of standard specifications [64], [65]. BP-ΣΔMs share much in common with their LP counterparts, except for the obvious difference that the quantization noise is suppressed around fn instead of dc. A common choice is fn=fs/4, i.e., just in the middle of the Nyquist band. It can be shown that this location optimizes the trade-off between antialiasing filtering and image-reject filtering in digital wireless transceivers [25]. Linked to the choice of fn=fs/4, BP-ΣΔMs architectures are obtained from LP-ΣΔMs by applying a LP-to-BP transformation method, which in the DT domain is formulated as z−1→−z−2. As a consequence of this transformation, the zeroes of the original LP NTF(z) are moved from dc to fs/4. Moreover, this transformation keeps all properties of the original LP-ΣΔMs.13
D. 대역통과 ΣΔ 변조기
대역통과(BP) ΣΔ 변조기는 NTF(f)의 영점을 중간 주파수(IF) 위치, 일반적으로 중심 또는 노치 주파수(fn) 주변의 주어진 대역폭에 배치하는 특정 클래스의 ΣΔ 변조기입니다. 따라서 BP-ΣΔ 변조기는 루프 필터가 저역통과(LP) 유형이 아닌 대역통과 유형으로 되어 있다는 점에서 LP 변조기와 다릅니다(그림 15 참조) [59]–[62]. 이는 무선 통신 시스템의 프론트 엔드에서 명백한 응용을 가집니다. 실제로, BP-ΣΔ 변조기는 나이퀴스트율 ADC와 비교하여 전체 나이퀴스트 대역(dc부터 fs까지)을 디지털화할 필요가 없기 때문에, 이러한 시스템에서 ADC 구현에 매우 적합합니다(그림 15 참조). 대신, 신호 대역만을 디지털화하여 주어진 DR을 얻기 위해 훨씬 적은 전력 소비가 필요합니다 [25], [63]. 또한, IF A/D 변환은 사중 혼합, 채널 선택, 이득 제어 및 복조를 포함한 대부분의 신호 처리를 아날로그 도메인에서 디지털 도메인으로 이동할 수 있게 합니다. 이는 프로그래밍 가능성과 다양한 표준 사양에 대한 적응성이 높은 견고한 라디오 주파수(RF) 수신기를 결과적으로 만들어냅니다 [64], [65]. BP-ΣΔ 변조기는 영점이 dc 대신 fn 주변에서 양자화 잡음이 억제된다는 명백한 차이를 제외하고는 LP 변조기와 많은 공통점을 가지고 있습니다. 일반적인 선택은 fn=fs/4로, 이는 나이퀴스트 대역의 중간에 위치합니다. 이 위치는 디지털 무선 송수신기에서 안티에일리어싱 필터링과 이미지 거부 필터링 간의 절충을 최적화한다는 것을 보여줄 수 있습니다 [25]. fn=fs/4의 선택과 연결된 BP-ΣΔMs 구조는 LP-ΣΔMs에서 LP-to-BP 변환 방법을 적용하여 얻어지며, DT 도메인에서는 z−1→−z−2로 공식화됩니다. 이 변환의 결과로, 원래 LP NTF(z)의 영점은 dc에서 fs/4로 이동합니다. 또한, 이 변환은 원래 LP-ΣΔMs의 모든 속성을 유지합니다.

The design and analysis of BP-ΣΔMs is the same as that of LP-ΣΔMs, but considering bandpass loop filters instead of lowpass loop filters. Indeed, it can be shown that the main figures of merit, i.e., in-band noise power, DR, SNR, SNDR have the same expressions as the ones obtained in previous sections. In practice, it means that a BP-ΣΔM can be synthesized by replacing integrators by resonators in the modulator loop filter as will be described in Section IV [6], [28], [66].
대역통과(BP) ΣΔ 변조기의 설계 및 분석은 저역통과(LP) ΣΔ 변조기와 같지만, 저역통과 루프 필터 대신 대역통과 루프 필터를 고려합니다. 실제로, 밴드 내 잡음 전력, 동적 범위(DR), 신호 대 잡음비(SNR), 신호 대 (잡음 플러스 왜곡) 비율(SNDR)과 같은 주요 성능 지표는 이전 섹션에서 얻은 것과 같은 수식을 가지고 있음을 보여줄 수 있습니다. 실제로 이는 제 IV장에서 설명될 것처럼 변조기 루프 필터에서 적분기를 공진기로 대체함으로써 BP-ΣΔM을 합성할 수 있음을 의미합니다 [6], [28], [66].
E. Continuous-Time ΣΔMs
E. Continuous-Time ΣΔMs
The majority of ΣΔMs reported so far have been implemented using DT circuit techniques, mostly based on switched-capacitor (SC) circuits [15]. However, the increasing demand for ever faster ADCs in broadband communication systems has boosted the interest in CT implementations. These modulators are able to operate at higher sampling rates with lower power consumption than their DT counterparts [10], [14], [66].
E. 연속 시간(CT) ΣΔ 변조기
지금까지 보고된 대부분의 ΣΔ 변조기들은 주로 스위치드-캐패시터(SC) 회로를 기반으로 하는 디지털 타임(DT) 회로 기술을 사용하여 구현되었습니다 [15]. 그러나 광대역 통신 시스템에서 더욱 빠른 ADC에 대한 수요가 증가함에 따라 연속 시간(CT) 구현에 대한 관심이 증가하고 있습니다. 이러한 변조기들은 그들의 DT 대응품보다 더 높은 샘플링 속도로 더 낮은 전력 소비로 작동할 수 있습니다 [10], [14], [66].
Looking at both architectures depicted in Fig. 8, one can see several differences between DT- and CT-ΣΔMs. Apart from the CT circuit nature of the loop filter, the most significant difference is related to the point where the sampling process takes place, which constitutes one of the key advantages of CT-ΣΔMs over their DT counterparts [14]. However, as both DT- and CT- signals are involved, the mathematical analysis (and consequently the synthesis) of CT-ΣΔMs becomes more difficult than in the case of DT-ΣΔMs [10], [28], [63], [66]–[68].
그림 8에서 보여진 두 아키텍처를 살펴보면, DT-ΣΔMs와 CT-ΣΔMs 사이에 몇 가지 차이점을 볼 수 있습니다. 루프 필터의 연속 시간(CT) 회로 성질을 제외하고, 가장 중요한 차이점은 샘플링 과정이 발생하는 위치와 관련이 있으며, 이는 CT-ΣΔMs가 그들의 DT 대응품에 비해 가지는 주요 장점 중 하나를 구성합니다 [14]. 그러나 DT 및 CT 신호 모두 관련되어 있기 때문에, CT-ΣΔMs의 수학적 분석(그리고 따라서 합성)은 DT-ΣΔMs의 경우보다 더 어려워집니다 [10], [28], [63], [66]–[68].
In order to understand the principles of operation underlying the signal processing involved in CT-ΣΔMs, let us consider the conceptual block diagram shown in Fig. 16(a). Note that the modulator output signal must be transformed from DT- to CT- in the feedback loop. This signal reconstruction is very critical and has a significant impact on the overall behavior of the modulator [28]. There are several DAC waveforms that can be used in CT-ΣΔMs. Fig. 17 shows a summary of the most representative possibilities including the nomenclature used for the feedback waveforms—extracted from [14]. Among others, the most commonly used DACs incorporate rectangular feedback pulses of basically three types: nonreturn-to-zero (NRZ) [Fig. 17(a)], return-to-zero (RZ) [Fig. 17(b)], and half-delay return-to-zero (HRZ) [Fig. 17(c)]. Their Laplace S-transforms can be generally written as
{{\rm DAC}(s)} = {e^{-sp_1T_s}-e^{-sp_2T_s} \over s} \eqno{\hbox{(11)}}
where (p1,p2)=(0,1),(0,1/2) and (1/2, 1) for NRZ, RZ, and HRZ DACs, respectively.
CT-ΣΔMs에서 관련된 신호 처리의 작동 원리를 이해하기 위해, 그림 16(a)에 표시된 개념적 블록 다이어그램을 고려해 봅시다. 변조기 출력 신호는 피드백 루프에서 디지털 타임(DT)에서 연속 타임(CT)으로 변환되어야 합니다. 이 신호 재구성은 매우 중요하며 변조기의 전체적인 동작에 큰 영향을 미칩니다 [28]. CT-ΣΔMs에서 사용할 수 있는 여러 DAC 파형이 있습니다. 그림 17은 피드백 파형에 사용된 명명법을 포함하여 가장 대표적인 가능성을 요약하여 보여줍니다—[14]에서 발췌됨. 그 중에서도 가장 일반적으로 사용되는 DAC은 세 가지 기본 유형의 직사각형 피드백 펄스를 포함합니다: 논리턴-투-제로(NRZ) [그림 17(a)], 리턴-투-제로(RZ) [그림 17(b)], 그리고 하프-딜레이 리턴-투-제로(HRZ) [그림 17(c)]. 그들의 라플라스 S-변환은 일반적으로 다음과 같이 쓸 수 있습니다:
DAC(s) = (e^(-sp1T_s) - e^(-sp2T_s)) / s (11)

여기서 (p1, p2)는 NRZ, RZ 및 HRZ DAC의 경우 각각 (0,1), (0,1/2), (1/2, 1)입니다.


Let us consider the transfer function for the DAC in (11) and the basic block diagram of the CT-ΣΔM shown in Fig. 16(a). Because of the presence of a S/H inside the loop, the input-output behavior of the noise shaping loop filter can be described by an equivalent DT transfer function, as illustrated in Fig. 16(b), given by
\eqalignno{{H(z)} &= {\cal Z}\left\{{\cal L}^{-1}[{\rm DAC}(s)H(s)]\left[\sum_{n=0}^{\infty}\delta(t-nT_s)\right] \right\} \cr &&\hbox{(12)}}
where Z{⋅} and L−1{⋅} stand for the Z- and inverse L-transform operators, respectively.
DAC의 전달 함수 (11)와 그림 16(a)에 표시된 CT-ΣΔM의 기본 블록 다이어그램을 고려해 보겠습니다. 루프 내부에 샘플-홀드(S/H)가 존재하기 때문에, 노이즈 셰이핑 루프 필터의 입력-출력 동작은 그림 16(b)에서 보여지듯이 등가의 DT 전달 함수로 설명될 수 있으며, 다음과 같이 주어집니다:
H(z) = Z{L^(-1)[DAC(s)H(s)][Σ from n=0 to ∞ of δ(t-nT_s)]} (12)

여기서 Z{⋅}과 L^(-1){⋅}은 각각 Z 변환 및 역 라플라스 변환 연산자를 나타냅니다. 이 식은 연속 시간 신호를 이산 시간 신호로 변환하는 과정에서 DAC와 루프 필터의 영향을 합성하여 이산 시간 시스템으로 표현합니다. 이 과정을 통해, CT-ΣΔM의 성능 특성을 분석하고 최적화할 수 있습니다.
Based on the equivalent DT loop filter transfer function shown in (12), the most usual procedure to design CT-ΣΔMs consists of, first, matching this equivalent filter with a reference DT loop filter chosen to fulfill the specifications; then, solving for the coefficients of the CT filter; and finally implementing this filter by CT circuits, usually based on Gm-C or active-RC building blocks. Careful choice of the CT filter structure is needed to have sufficient degrees of freedom to implement the reference DT loop filter [63]. In theory, any arbitrary ΣΔM topology, either single-loop or cascade, can be synthesized using a DT-to-CT transformation method. As an illustration, Fig. 18 shows a cascade 2-1 CT-ΣΔM obtained using such a method with its equivalent DT-ΣΔM [14].
(12)에 표시된 등가 DT 루프 필터 전달 함수를 기반으로, CT-ΣΔMs 설계의 가장 일반적인 절차는 먼저, 이 등가 필터를 명세를 충족시키기 위해 선택된 참조 DT 루프 필터와 일치시키는 것입니다. 그 다음에는 CT 필터의 계수를 구하고, 마지막으로 주로 Gm-C 또는 액티브-RC 빌딩 블록을 기반으로 하는 CT 회로를 사용하여 이 필터를 구현합니다. 참조 DT 루프 필터를 구현하기 위한 충분한 자유도를 갖기 위해 CT 필터 구조를 신중하게 선택할 필요가 있습니다 [63]. 이론적으로, 단일 루프나 캐스케이드 등 임의의 ΣΔM 토폴로지는 DT-to-CT 변환 방법을 사용하여 합성될 수 있습니다. 예를 들어, 그림 18은 이러한 방법을 사용하여 얻은 캐스케이드 2-1 CT-ΣΔM과 그에 상응하는 DT-ΣΔM을 보여줍니다 [14].

The main problem of using the DT-to-CT synthesis method is that it usually yields an increase of the analog circuit complexity, with the subsequent penalty in sensitivity to technology parameter variations. This is particularly critical in the case of cascade CT-ΣΔM topologies, where—in order to get a functional modulator while keeping the digital cancellation logic of the original DT-ΣΔM—every integrator and DAC output must be connected to the integrator input of later stages [14].
DT-to-CT 합성 방법을 사용하는 주된 문제는 일반적으로 아날로그 회로의 복잡성이 증가하며, 이는 기술 파라미터 변화에 대한 민감성 증가로 이어집니다. 이는 특히 캐스케이드 CT-ΣΔM 토폴로지의 경우에 매우 중요한 문제입니다. 여기서는 원래 DT-ΣΔM의 디지털 취소 논리를 유지하면서 기능적인 변조기를 얻기 위해 모든 적분기 및 DAC 출력이 후속 단계의 적분기 입력에 연결되어야 합니다 [14].
An alternative method for the design of the loop filter uses the desired NTF(f) as a starting point. This synthesis method is often referred to as direct CT synthesis method. Usually, an inverse Chebychev distribution of the NTF(f) zeroes is considered because it has advantages in terms of SNR and stability. Once the desired NTF(f) has been chosen, the loop filter can be derived from the linearized model [10]. Indeed, it can be shown that applying the direct-synthesis method to cascade CT-ΣΔMs, more efficient architectures are obtained in terms of loop filter optimization, analog circuitry complexity, power consumption, and robustness to circuit element tolerance errors [69].
루프 필터 설계의 대안적인 방법은 원하는 NTF(f)를 시작점으로 사용하는 것입니다. 이 합성 방법은 종종 직접 CT 합성 방법으로 언급됩니다. 일반적으로 NTF(f)의 영점에 대해 역 체비셰프 분포가 고려되는데, 이는 SNR과 안정성 측면에서 이점이 있기 때문입니다. 원하는 NTF(f)가 선택되면, 루프 필터는 선형화된 모델로부터 유도될 수 있습니다 [10]. 실제로, 직접 합성 방법을 캐스케이드 CT-ΣΔMs에 적용함으로써, 루프 필터 최적화, 아날로그 회로의 복잡성, 전력 소비, 그리고 회로 요소 허용 오류에 대한 견고성 측면에서 보다 효율적인 아키텍처가 얻어짐을 보여줄 수 있습니다 [69].
https://ieeexplore.ieee.org/document/5672380
Sigma-Delta Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey
This paper presents a tutorial overview of <formula formulatype="inline" xmlns:mml="http://www.w3.org/1998/Math/MathML" xmlns:xlink="http://www.w3.org/1999/xlink"> <tex Notation="TeX">$\Sigma\Delta$</tex></formula> modulators, their operating principles an
ieeexplore.ieee.org
'시스템 반도체 설계 > Sigma-Delta Modulators' 카테고리의 다른 글
| [DSM] 논문 : Sigma-Delta Modulators (5) (1) | 2024.09.14 |
|---|---|
| [DSM] 논문 : Sigma-Delta Modulators (4) Nonideal Performance and Systematic Design (1) | 2024.09.13 |
| [DSM] 논문 : Sigma-Delta Modulators (2) Fundamentals of ΣΔ Modulators (1) | 2024.09.11 |
| [DSM] 논문 : Sigma-Delta Modulators (1) Introduction (1) | 2024.09.10 |
| [ΣΔMs] Sigma-Delta Modulators 의 기본 구조 (0) | 2024.02.28 |


