공부중
[DSM] DSM 동작 구조 예시 - 카페 시스템 (2) 본문
2025.05.01 - [시스템 반도체 설계/Sigma-Delta Modulators] - [DSM] DSM 동작 구조 예시 - 카페 시스템 비유 (1)
앞에서 DSM 동작에 대해 예시를 들어 알아보았다. 이번 글에서는 입력신호에 따른 출력에 대해 생각해보자.
1. DC 입력
1.1 VDD에 해당하는 DC 입력이 있다고 보자.
앞의 예시에서 커피 금액이 5000원인것이다.
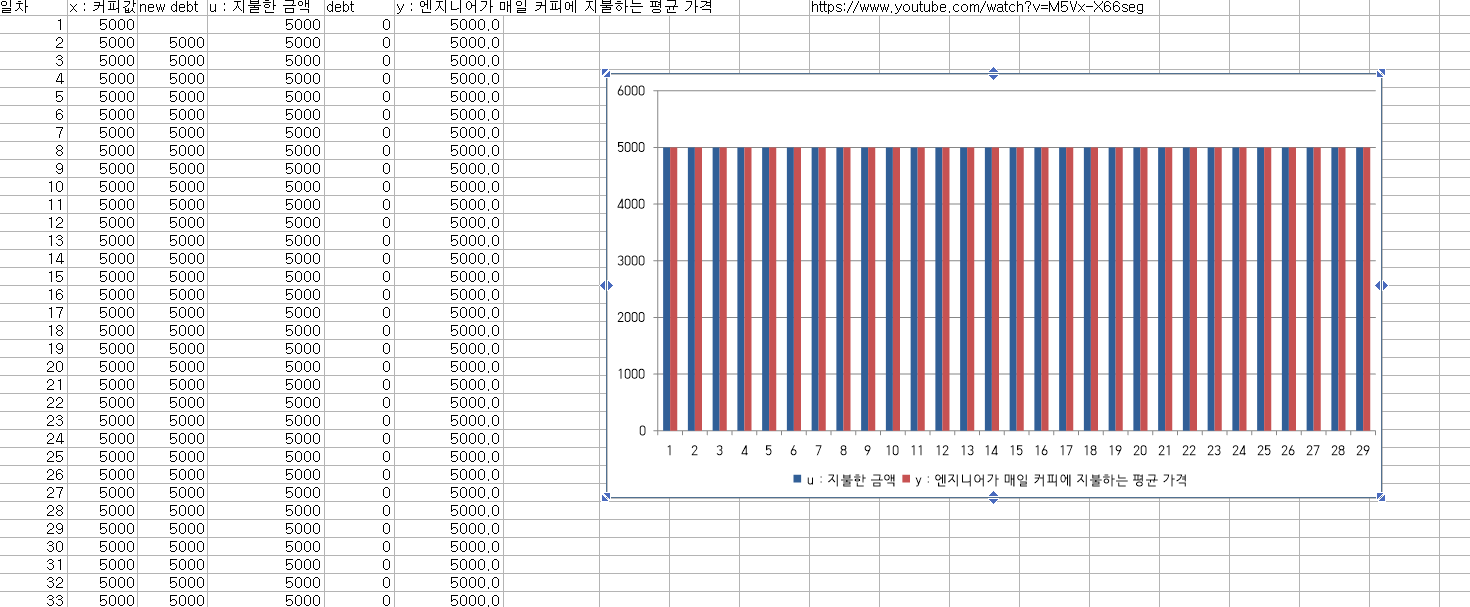
그러면 비트트림 결과가 다음과 같이 나올 것이다
| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ..... |
1.2 입력이 dc = 0인 경우
커피가 0원이라 할 수 있다.
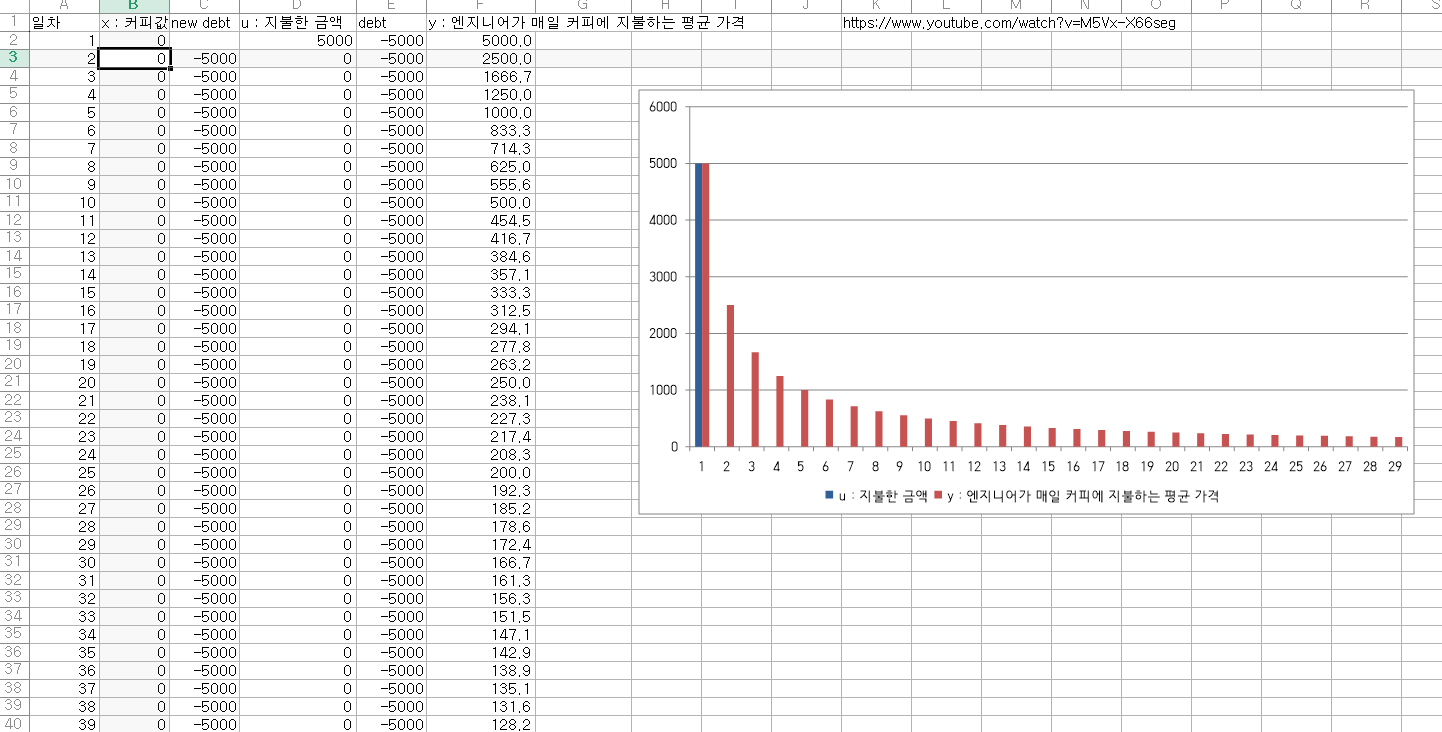
그럼 출력이 다음과 같이 나올 것이다.
| 1 0 0 0 0 0 0 0 0 0 0 0 0 0 ... |
1.3 적당한 임의의 값일 경우
커피 금액이 3000원이면, 평균 낸 금액이 3000원에 수렴하도록 돈을 내게 된다.
입력이 중간값이면 평균을 맞추려고 한다는 것이다.
3000원을 정확히 낼 수는 없으며, 오차를 누적하며 5000원이나 0원을 내는 것이고, 이로인해 출력이 1과 0 사이를 왔다갔다 하게 될 것이다.
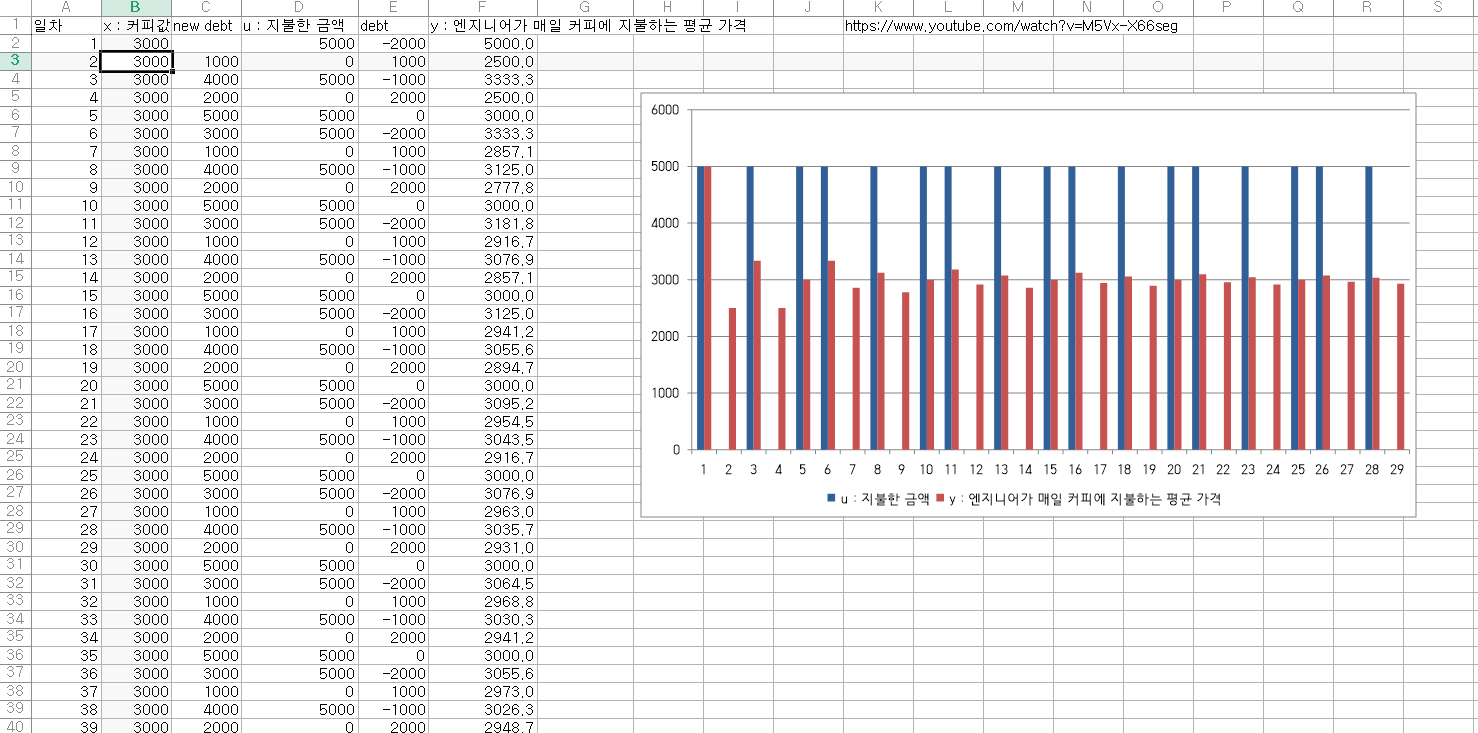
즉 다음과 같은 출력이 나온다.
| 1 0 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 |
1.4 결론
DSM은 입력이 DC더라도, 출력이 ±1만 가능하기 때문에, 그 평균값을 맞추기 위해 1과 0을 섞어서 표현한다.
즉, DSM은 "아날로그 평균값"을 비트의 local 평균 (density)으로 재현한다는 것이다.
2. 주기 입력
앞에서 확인한 DC가 아니라 sin과 같은 주기함수라면 어떻게 될까?
우선 커피값을 sin으로 바꾸기는 너무 힘드니까 증가하는 어떤 값을 확인해보자 (아래 사진은 정확하지 않다)

아래와 같이 변동되는 값에 대해서 우리는 평균을 다시 설정하여야 한다.
지금까지는 0부터 n 까지의 평균을 내서 해당 커피값을 맞추려 했지만,
점점 증가하거나, 감소하는 주기적인 값에 대해서 이런식으로 설정하게 된다면 극단적으로 오차들의 평균이 2500원에 가까워지며, 2500이라는 값만 나타내버리게 될 수도 있을 것이다.
즉, 입력 신호가 점차 증가하거나 감소하는 주기적인 파형(예: 사인파)인 경우, 단순히 0부터 n까지 전체 평균을 계산하는 방식으로는 실제 입력의 시간에 따른 변화를 반영하지 못하고, 오히려 평균값이 **고정된 특정 값(예: 2500)**에 수렴하는 문제가 발생할 수 있다.
따라서 이러한 입력을 정확히 복원하려면, 고정된 길이의 구간(window)을 설정하고, 그 구간 안에서 이동 평균(sliding average)을 계산해야 한다.
그렇기 때문에 입력 사인파를 복원하려면 일정 구간을 평균 내야 한다.
2.1 구간 설정 기준
gpt 말로는 다음과 같은 3가지 방법이 있다고 제시하고 있는데 OSR로 하는게 맞는거 같다.
1. Oversampling Ratio (OSR) 기준 2. 사인파 주기의 일정 부분 (Sliding Window)  3. 디지털 필터 통과대역에 따라 설정 디지털 decimation 필터에서:
|
2.2 Oversampling Ratio (OSR)란?
입력 신호 대역폭보다 훨씬 높은 속도로 샘플링하는 비율을 의미한다.

그러니까 1.28M/2*5k를 하면 128이며, 나이퀴스트 기준보다 128 배 더 빠르게 샘플링한다는 것이다.
DSM에서는 오버 샘플링해서 양자화 잡음이 넓은 주파수 대역에 퍼지고, 저주파대역에는 노이즈가 희석되게 된다.
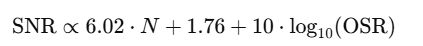
이므로 OSR을 높여 SNR을 높일 수도 있다.
'시스템 반도체 설계 > Sigma-Delta Modulators' 카테고리의 다른 글
| [DSM] delta sigma Modulator 구조 이해 - Simulink (0) | 2025.05.19 |
|---|---|
| [DSM] DSM 동작 구조 예시 - 카페 시스템(3) 노이즈 쉐이핑 (0) | 2025.05.07 |
| [DSM] DSM 동작 구조 예시 - 카페 시스템 비유 (1) (1) | 2025.05.05 |
| [DSM] 논문 : Sigma-Delta Modulators (5) (1) | 2024.09.14 |
| [DSM] 논문 : Sigma-Delta Modulators (4) Nonideal Performance and Systematic Design (1) | 2024.09.13 |


